ABSTRACT

This paper focuses on optimizing scheduling solutions for the flexible flow shop problem, with tooling constraints and machine eligibility, to minimize makespan for cultivating sugarcane. Normally, preparing the soil for planting sugarcane requires six steps: 1) 7 power harrow and rototiller, 2) rotary mini combine, 3) 22/24 disc harrow, 4) rotary mini combine, 5) sugarcane plantation, and 6) sugarcane sprayer. Each of these steps requires a variety of tools. With limited availability of tools and equipment, resource allocation is important. The objective of this research was to minimize the makespan. For optimal convergence, meta-heuristics, such as a Differential Evolution algorithm, a Particle Swarm optimization algorithm, and a Hybrid DEPSO algorithm were developed to solve the problem. Experimental results showed that all three methods efficiently solved flexible flow shop problems.

Keywords: Scheduling, Tool limitations, Tooling constraints, Tool change, Differential evolution, Particle swarm optimization, Sugarcane

INTRODUCTION

Sugarcane is an important crop in Thailand, the second largest sugar exporter in the world (Office of the Cane and Sugar Board, 2016). Increasing demand for cultivating sugarcane in Thailand has outstripped resources, especially for small farmers who do not own their own agricultural machinery. Preparing the fields for planting requires hiring large and expensive operators (Prasara and Gheewala, 2016). Thus, better allocation of resources is important to reduce the cost of producing sugarcane (Sugar Research Australia, 2017).

Preparing the soil for sugarcane production involves six steps, denoted here by the principal tool required: 1) 7 power harrow and rototiller, 2) rotary mini combine, 3) 22/24 disc harrow, 4) rotary mini combine, 5) sugarcane plantation, and 6) sugarcane sprayer. Steps 1, 4, 5, and 6 require small tractors and Steps 2 and 3 require medium- to large-sized tractors (see Figure 1). This study attempts to find solutions to the scheduling challenges inherent in sugarcane cultivation created by these resource/machinery constraints, with the objective of minimizing completion time. The constraints include flexible flow shop, the need for the same machine at multiple steps, and limited tools.

Many researchers have presented a variety of flexible flow shop models based on the traditional flexible flow shop scheduling problem. The flexible flow shop problem is an NPhard problem, and metaheuristic algorithms have been presented as the most optimal way to handle such large problems (Hoogeveen et al., 1996; Gupta et al., 2002; Wang and Hunsucker, 2003; Baumann and Trautmann, 2011). Many algorithms have been designed to help solve these problems, including tabu search algorithms (Widmer, 1991), hybridization of particle swarm optimization with Cauchy distribution for optimal sequences (Sangsawang et al., 2015), a modified genetic algorithm for hybridized ant colony optimization (Chamnanlor et al., 2017), and a simulated annealing based heuristic (Batur et al., 2016). Flexible flow shop problems are complex. Several applied mathematical models and metaheuristics have been developed as solutions, such as those by Melnyk et al. (1989), Widmer (1991), Ghosh et al. (1992), Gultekin et al. (2006), Chen (2008), Zhonghua et al. (2009), Zeballos (2010), Zeballos et al. (2010), Xu et al. (2013), and Özpeynirci et al. (2016). Recent research has applied evolutionary computing methods. Differential evolution is one of the strongest methods for continuous optimization, with an algorithm that has been successfully applied with several techniques. For example, Zhou (2012) used the new differential evolution algorithm based on a variable neighborhood search to contribute toward solving the flow shop scheduling problem. Tonge and Kulkarni (2013) improved the differential evolution algorithm using the classical Nawaz Enscore Ham algorithm and iterated local search, with an enhanced swap operator to minimize makespan. Many researchers have used differential evolution algorithms to minimize makespan (Rahman et al., 2014; Moonsri et al., 2015; Santosa and Riyanto, 2016). The particle swarm optimization algorithm is another interesting method (Liang et al., 2006; Nasir et al., 2012). This technique was first proposed by Eberhart and Kennedy (1995) and provides simple instrumentality that has been successfully employed in many areas of research. Additionally, much research on the particle swarm optimization algorithm has focused on diversifying the search to prevent premature convergence and allow the algorithm to escape from local minima (Shi and Eberhart, 1998; Yang and Simon, 2005). Currently, the literature combines particle swarm optimization and iterated local search to solve hybrid flow shop scheduling problems with preventive maintenance activities (Li et al., 2014). To increase performance and alleviate the defects of problem solving, the hybrid DEPSO algorithm has been proposed (Jayabarathi, 2007; Li et al., 2008; Pant et al., 2008).

This paper proposes a solution that applies differential evolution, particle swarm optimization, and hybrid DEPSO to the problem of tractor scheduling, with the objective of minimizing the makespan. The results from this study can serve as a prototype for developing decision tools for sugarcane cultivation and can also be applied to other industrial crops.

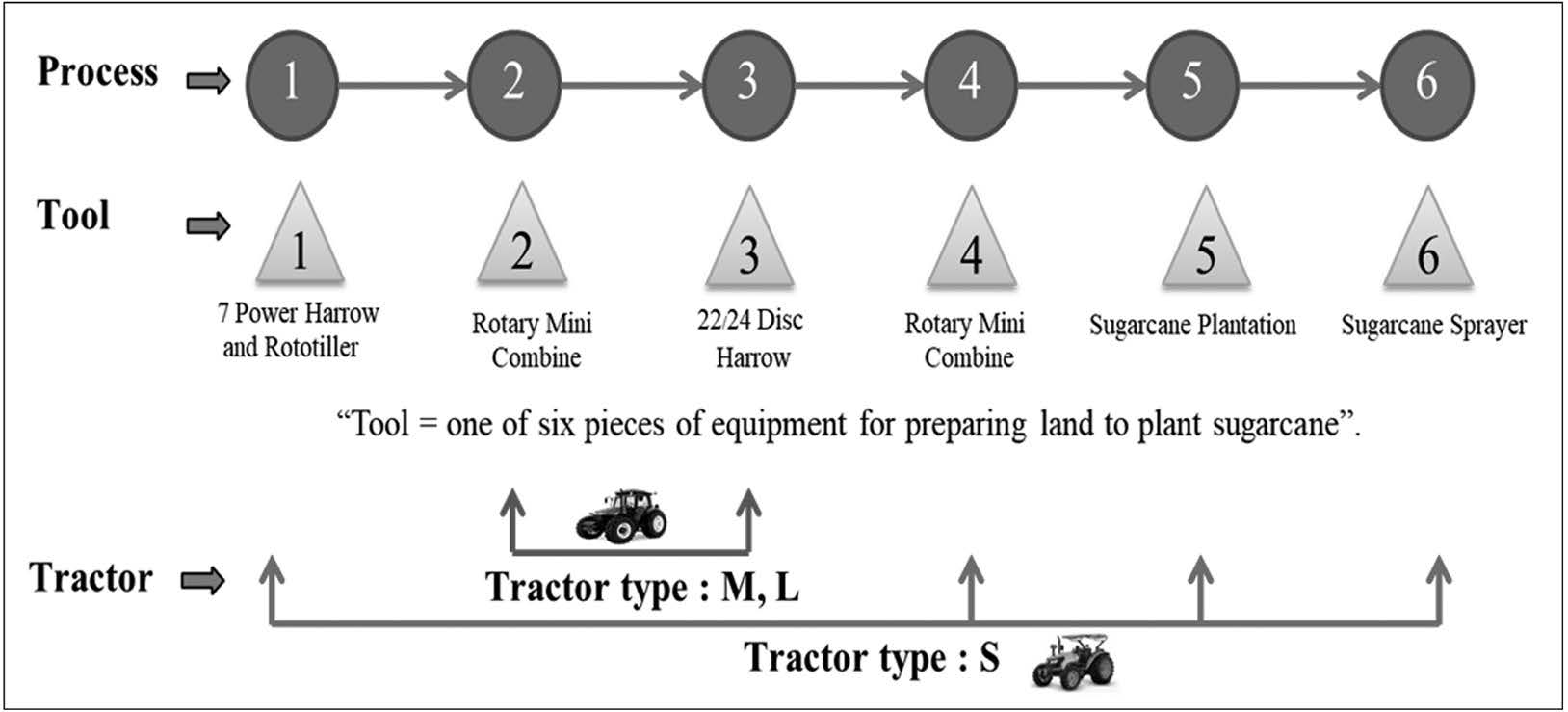
Figure 1. Characteristics of the problem.

MATERIALS AND METHODS

Differential evolution algorithm

Storn and Price (1997) developed the differential evolution algorithm for continuous optimization problems:

Notation:
G :             Generation number
P_G :            Population of NP-D-dimension
X_i.G :           Random vector
V_i.G :           Mutant vector
Ui.G :          Trial vector
D :              Dimensional parameter
randb (j) :    A random number generated from [0,1]
rnbr (I) :      A random integer from [1, 2,…, D]
J_rand :         Position vector of particle i
F :              Scaling factor

Differential evolution:

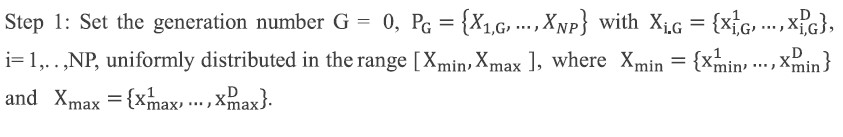
Mutation operation. Each of the N parameter vectors undergoes mutation, recombination, and selection. Mutation expands the search space. For a given parameter vectorX_i,G, randomly select three vectors X_1,G, X_2,G, …, X_3,G, such that the indices I, r1, r2, r3 are distinct. Add the weighted difference of two of the vectors to the third V_i,G = X_r1,G+ F(X_r2,G-X_r3,G). The mutation factor F is a constant from [0,2]. V_i,G is called the donor vector.

Recombination operation. Recombination incorporates successful solutions from the previous generation. The trial vector U_i,G+1 is developed from the elements of the target vector, X_i,G, and the elements of the donor vector, V_i,G+1. Elements of the donor vector enter the trial vector with probability CR..

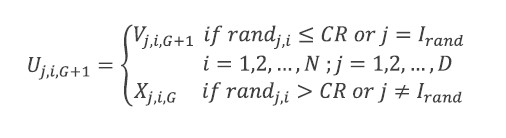
rand_j,i~U[0,1], I_rand is a random integer from [1,2,…,D]. I_rand ensuring that V_i,G+1 ≠ X_i,G.

Selection operation. The target vectorX_i,G, is compared with the trial vector V_j,i,G+1 and the one with the lowest function value is admitted to the next generation.

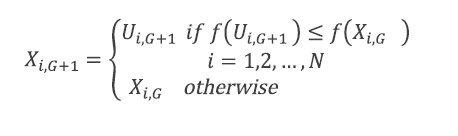
Mutation, recombination, and selection continue until some stopping criterion is reached; in the example, NP=100; F is 2; and CR is 0.8. Distances are given in Table 1.

Particle swarm optimization algorithm

Eberhart and Kennedy (1995) developed a novel optimization algorithm named particle swarm optimization that mimicked the flying behavior of a flock of birds; the algorithm has been verified as efficient for solving both continuous and discrete optimization problems (Figure 2).

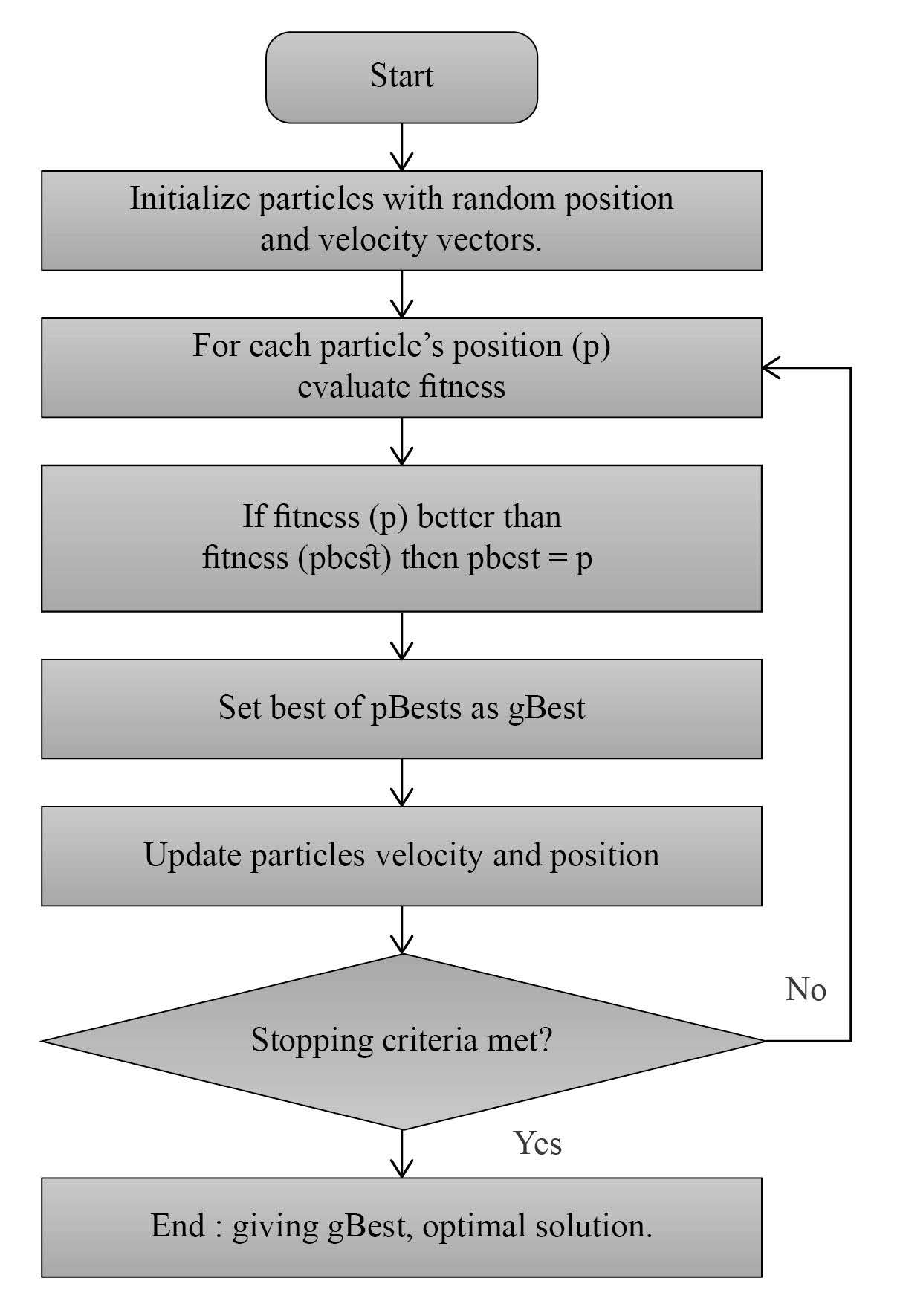
Figure 2. Flowchart of particle swarm optimization algorithm.

The structure of the particle swarm optimization algorithm is as follows:

Notation:
cp :           the particle best acceleration constant
cg :           the global best acceleration constant
w :            the inertia weight
r :             uniform random number in range [0,1]
xi :            the position vector of particle i
vi :            the velocity vector of particle i
pBest_i :      the personal best of the particle i
gBest :      the global best

Hybrid diff erential evolution and particle swarm optimization

Pant et al. (2008) developed the hybrid DEPSO algorithm to solve continuous optimization problems, helping to maintain population diversity and producing a good optimal solution. All algorithms used the same encoding-decoding algorithm.

The encode method. The operation vectors show each candidate solution for the flexible flow shop scheduling with tooling constraints problem. Encoding of each vector is randomly numbered from 0 to 1 as a real number. According to the size of the population considered, each vector has a dimension value equal to the number of fi elds considered, as shown in Figure 3.

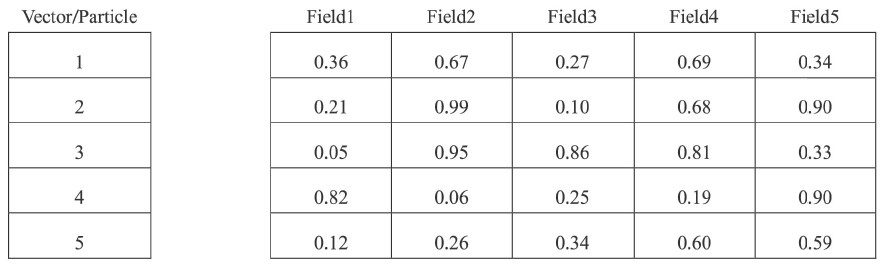
Figure 3. Operation-based encoding.

The pseudo code of the hybrid DEPSO Algorithm is:

Notation:
G :              Generation number
P_G :             Population of NP-D-dimension
X_i.G :           Random vector
V_i.G :           Mutant vector
U_i.G :           Trial vector
D :               Dimensional parameter
randb (j) :     A random number generated from [0,1]
rnbr (i) :       A random integer from [1,2,…,D]
J_rand :         Position vector of particle i
F :               Scaling factor
cp :             Particle best acceleration constant
cg :            The global best acceleration constant
w :             Inertia weight
r :              Uniformly random number in range [0,1]
xi :             Position vector of particle i
vi :             Velocity vector of particle i
pBest_i :       Personal best of the particle i
gBest :       Global best

The decode method. Decoding sorts the rank order value of each vector in ascending order. The vectors will assign the sequence of operations of the machine. The next step is the allocation of fields to machines. Fields will be allocated randomly to the machines at each stage by following the sequence of operations in the rank order value steps. For example, the assignment of five fields on a two-stage production system with two machines in each stage is sequenced as follows: field 3 - field 5 - field 1 - field 2 - field 4, as shown in Figure 4.

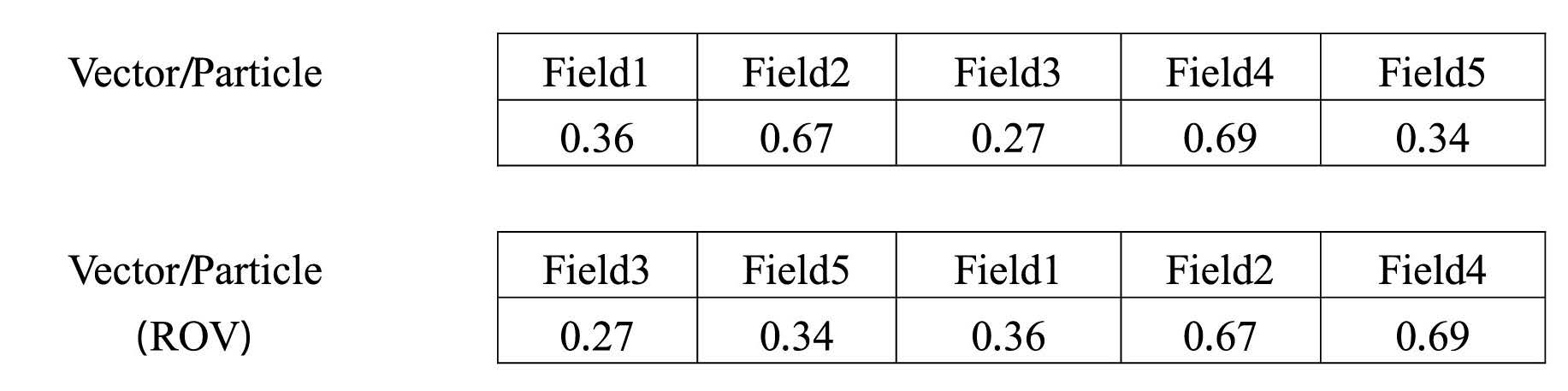
Figure 4. An example of decoding performed by sorting the rank order value.

After the random vectors/particles are sorted, the field sequence and machine assignment for each field must be assigned. Then, changing setup tool time and machine eligibility can be assigned simultaneously for calculating the completion time. Random machines are assigned to fields that minimize completion time. Moreover, fields are assigned to the machine that minimizes the completion time, as shown in Figure 5.

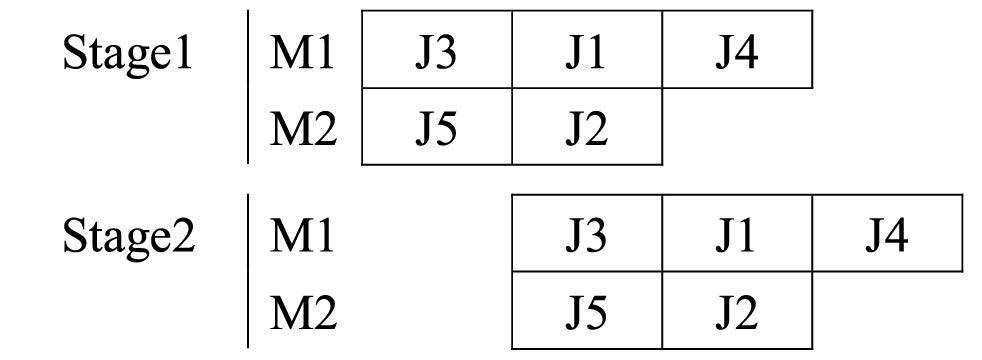
Figure 5. Decoding the particle to active scheduling.

Computational experiments

In this section, several computational experiments are reported from various test problems. The case has been established based on the number of fields (n), number of stages (s), and number of machines (m). Each case can be identified in the form of ‘‘Number of stage × Number of machines in each stage × Number of products’’. For instance, a problem with six stages, two machines at the first stage, two machines at the second stage, three machines at the third stage, two machines at the fourth stage, two machines at the fifth stage, and two machines at the sixth stage with 10 fields can be denoted by ‘‘6 x (2-2-3-2-2-2) x 10”. Consider the makespan with six stages to be processed on three types of tractors with six types of tools. The processing times, tool change times of types 1, 4, 5, and 6 and tool change times of types 2 and 3 are shown in Tables 1, 2, and 3. The experiments run for 10 replications.

Table 1. Data used in the experiments.

Table 2. Data used in tool change time of types 1, 4, 5, and 6.

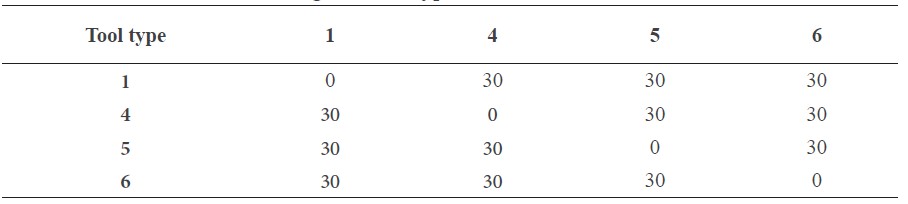
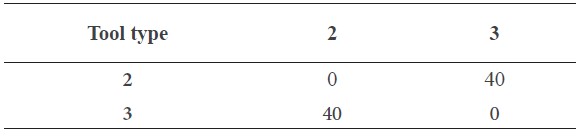
Table 3. Data used in tool change time of types 2 and 3.

Pilot experiments were performed to test a set of potential values for each parameter to find the appropriate differential evolution algorithm and particle swarm optimization parameters. The parameter values used in this paper are presented in Tables 4, 5, and 6.

Table 4. Parameter values for the differential evolution algorithm.

Table 5. Parameter values for the particle swarm optimization algorithm.

Table 6. Parameter values for the hybrid DEPSO algorithm.

RESULTS

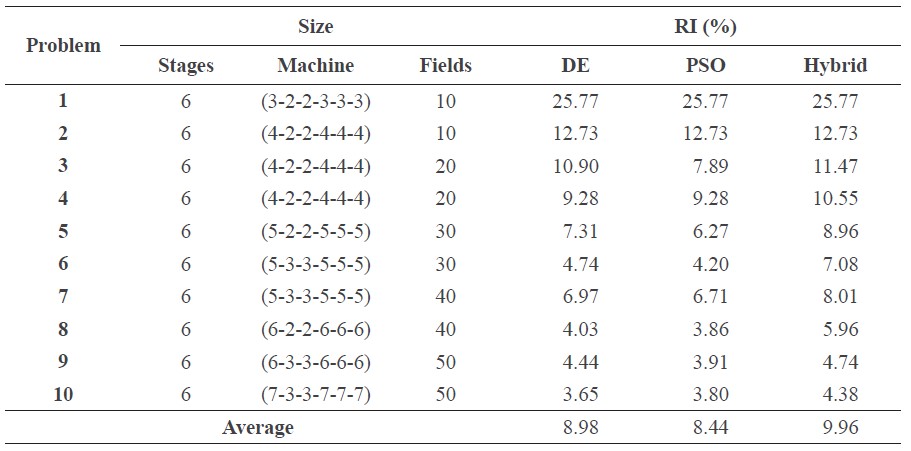
This section compares findings from the differential evolution algorithm, particle swarm optimization, and hybrid DEPSO algorithms that were created with 10 different problem sets: Set 1 – 6×(3-2-2-3-3-3)×10; Set 2 – 6×(4-2-2-4-4-4)×10; Set 3 – 6×(4-2-2-4-4-4)×20; Set 4 – 6×(4-2-2-4-4-4)×20; Set 5 – 6×(5-2-2-5-5-5)×30; Set 6 – 6×(5-3-3-5-5-5)×30; Set 7 – 6×(5-3-3-5-5-5)×40; Set 8 – 6×(6-2-2-6-6-6)×40; Set 9 – 6×(6-3-3-6-6-6)×50; Set 10 – 6×(7-3-3-7-7-7)×50. The computational results with the averages and the best solution obtained by the proposed algorithms are presented in Table 7; the hybrid DEPSO had a better makespan solution than the differential evolution algorithm and particle swarm optimization for eight of the problems. The hybrid method demonstrated an outstanding ability to solve flexible flow shop problems. The relative improvement results showed that the differential evolution algorithm, particle swarm optimization, and hybrid DEPSO algorithms improved the makespan solution by averages of 8.98%, 8.44%, and 9.96%, respectively (Table 8). While the hybrid DEPSO gave the best solution, its computational time was relatively high (Table 7, Figure 6), although at an acceptable level.

To measure the quality of makespan solution generated by the proposed algorithms, the relative improvement of the makespan solutions obtained by the current practice algorithm with respect to those of the differential evolution algorithm, particle swarm optimization, and hybrid DEPSO algorithms were calculated using equation (1). All algorithms were developed using MATLAB software, version 7.7.0.471 (R2008b) on Intel® Core(TM) i7-6700HQ CPU @ 2.80 GHz RAM (8 GB RAM).

Where,
RI = the relative improvement (%) between sol_current and sol_metaheuristic,

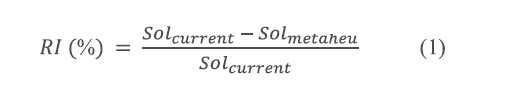
Sol_current = the solution obtained from the current practice, and
Sol_metaheu = the solution obtained from the differential evolution algorithm, particle swarm optimization or hybrid DEPSO algorithm

Table 7. Solution quality in terms of the objective function.

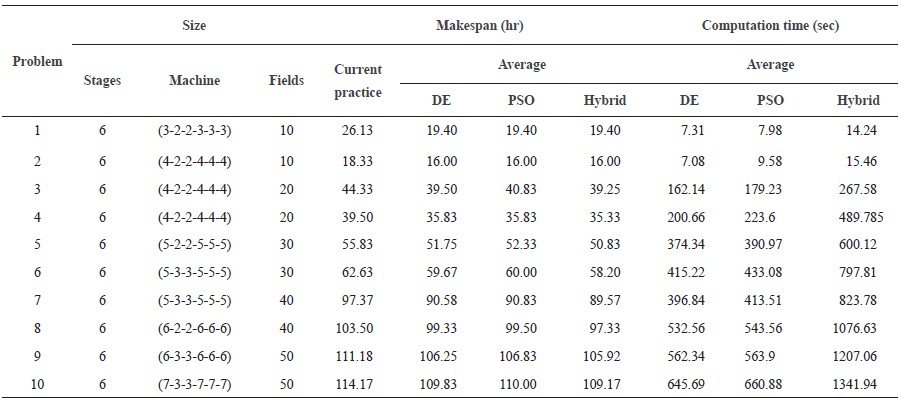
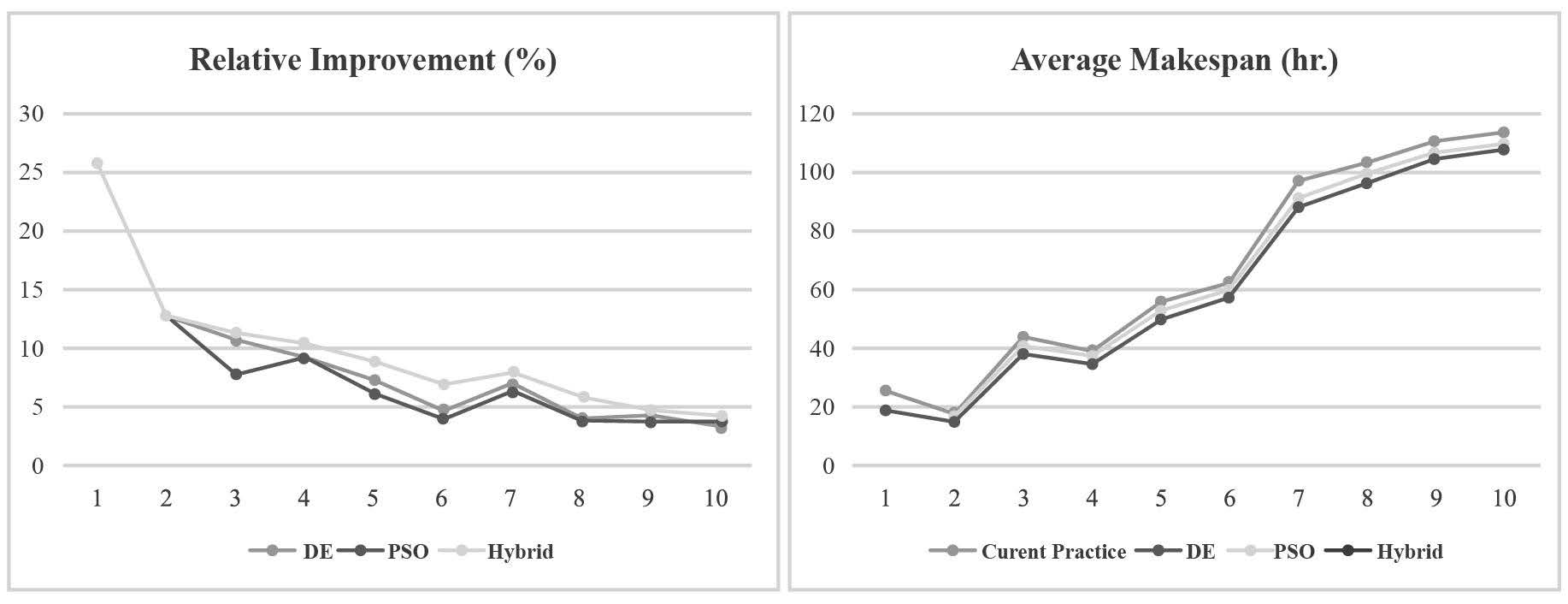
Figure 6. Percentage relative improvement and makespan for each test problem.

Table 8. Percentage relative improvements for each algorithm.

DISCUSSION

The sugarcane cultivation process is very complicated. We addressed the limitations of sugarcane cultivation, such as tooling constraints (setup time was considered as tool changing time only) and machine eligibility. An efficient scheduling method is an important problem in academic and industrial research.

In scheduling flexible flow shop problems, Baumann and Trautmann (2011) developed mixed integer programming for minimizing changeover times, but this method can only solve small problems. Chamnanlor and Sethanan (2015), Chamnanlor et al. (2017), and Sangsawang et al. (2015) developed hybrid particle swarm optimization with a Cauchy distribution for the optimal sequencing of problems involving a reentrant hybrid flow shop scheduling problem with time window for minimizing makespan. Batur et al. (2016) used a simulated annealing based heuristic for scheduling problems arising in hybrid flexible flow shop problems that repeatedly produce a set of multiple part types. Although most tooling constraint studies have looked at different problems, they have similar objectives, such as minimizing makespan or minimizing completion time (Melnyk et al. (1989), Widmer (1991), Widmer (1991), Ghosh et al. (1992), Gultekin et al. (2006), Chen (2008), Zeballos (2010), Zeballos et al. (2010), Xu et al. (2013)). This study found that the differential evolution algorithm, particle swarm optimization and hybrid DEPSO were effective and could allocate resources for sugarcane cultivation scheduling: all algorithms found better solutions than the current practice. Our performance comparison between the differential evolution algorithm and particle swarm optimization showed that the differential evolution algorithm performed better than particle swarm optimization in terms of quality, resolution and computation time, while hybrid DEPSO algorithms provided better answers than the differential evolution algorithm and the particle swarm optimization algorithm, which took more time to compute. The superiority of hybrid DEPSO over the differential evolution algorithm and particle swarm optimization has also been demonstrated in other research fields, such as flexible flow shop scheduling (Chamnanlor et al. (2017), Sangsawang et al. (2015), Batur et al. (2016)) and hybrid DEPSO algorithms (Jayabarathi et al. (2007), Li et al. (2008), Li et al. (2014)).

As sugarcane cultivation has only six steps, other cultivation systems may not be able to apply this research directly. Our solution is suitable for smallholder farmers that either do not own their own equipment or with insufficient tractors and tools to improve the soil for growing sugarcane.

CONCLUSION

This paper has presented the implementation of a particle swarm optimization algorithm and a differential evolution algorithm for optimizing multistage flexible flow shop scheduling problems in the sugar industry with dependent tooling constraints and machine eligibility constraints. The objective is to minimize the makespan. A differential evolution algorithm, a particle swarm optimization algorithm and a hybrid DEPSO algorithm were developed to solve practical problems. The differential evolution algorithm and the particle swarm optimization algorithm were compared to evaluate the effectiveness of the heuristics algorithm from real-world cases of planting sugarcane. This paper showed that the differential evolution algorithm gave an RI of makespan of 8.98%, the particle swarm optimization algorithm gives a RI of makespan of 8.44% and the hybrid DEPSO algorithm gives a RI of makespan of 9.96%.

Although the hybrid DEPSO algorithm demonstrated an outstanding ability to solve the problem, it is possible to modify the differential evolution algorithm or the particle swarm optimization algorithm and use other meta-heuristics or hybrid methods to improve solutions. All three methods could minimize the makespan. The hybrid DEPSO algorithm gave the best answer by reducing the time to complete the work by 9.96% relative to current practice. Future research should consider the start time of machines for cultivation and include the distance between field i and field j for each cultivation process. The approach applied in this study can extended to other other agricultural industries.

ACKNOWLEDGEMENTS

This work was supported by the Research Unit on System Modeling for Industry (Grant No. SMI. KKU PHD591005), Industrial Engineering Department, Faculty of Engineering, Khon Kaen University, Thailand. We thank Ian Thomas for linguistic corrections. 

REFERENCES

Batur, G.D., Erol, S., and Karasan, O.E. 2016. Robot move sequence determining and multiple part-type scheduling in hybrid flexible flow shop robotic cells. Computers & Industrial Engineering. 100: 72-87. https://doi.org/10.1016/j.cie.2016.08.006

Baumann, P., and Trautmann, N. 2011. A continuous-time MILP to compute schedules with minimum changeover times for a make and pack production. International Journal of Production Research. 51(6): 1707-1721. https://doi.org/10.1080/00207543.2012.694489

Chamnanlor, C., and Sethanan, K. 2015. Bi-objective Optimization for Reentrant Shop Scheduling Problem. Chiang Mai University Journal of Natural Sciences Special Issue on Logistics and Supply Chain Systems. 14(4S): 447-459. https://doi.org/10.12982/cmujns.2015.0098

Chamnanlor, C., Sethanan, K., Gen, M., and Chien, C.F. 2017. Embedding ant system in genetic algorithm for re-entrant hybrid flow shop scheduling problems with time window constraints. Journal of Intelligent Manufacturing. 28(8): 1915-1931. https://doi.org/10.1007/s10845-015-1078-9

Chen, J.S. 2008. Optimization models for the tool change scheduling problem. Omega. 36(5): 888-894. https://doi.org/10.1016/j.omega.2006.04.006

Eberhart, R., and Kennedy, J. 1995, October. A new optimizer using particle swarm theory. p. 39-43. In Micro Machine and Human Science, 1995. MHS'95 (eds) Proceedings of the Sixth International Symposium IEEE. 4-6 Oct. 1995. https://doi.org/10.1109/MHS.1995.494215

Ghosh, S., Melnyk, S.A., and Ragatz, G.L. 1992. Tooling constraints and shop floor scheduling: evaluating the impact of sequence dependency. International Journal of Production Research. 30(6): 1237-1253. https://doi.org/10.1080/00207549208942954

Gupta, J.N.D., Krger, K., Lauff, V., Werner, F., and Sotskov, Y.N. 2002. Heuristics for hybrid flow shops with controllable processing times and assignable due dates. Computers & Operations Research. 29(10): 1417–1439. https://doi.org/10.1080/00207543.2012.737942

Gultekin, H., Akturk, M.S., and Karasan, O.E. 2006. Cyclic scheduling of a 2-machine robotic cell with tooling constraints. European Journal of Operational Research. 174(2): 777-796. https://doi.org/10.1016/j.ejor.2005.03.021

Hoogeveen, J.A., Lenstra, J.K., and Veltman, B. 1996. Preemptive scheduling in a two-stage multiprocessor flow shop is NP-hard. European Journal of Operational Research. 89(1): 172-175. https://doi.org/10.1016/S0377-2217(96)90070-3

Jayabarathi, T., Chalasani, S., Shaik, Z.A., and Kodali, N.D. 2007. Hybrid differential evolution and particle swarm optimization based solutions to short term hydro thermal scheduling. WSEAS Transactions on Power Systems. 11: 245-254. https://doi.org/10.1016/j.asoc.2007.10.006

Li, B.B., Wang, L., and Liu, B. 2008. An effective PSO-based hybrid algorithm for multiobjective permutation flow shop scheduling. IEEE transactions on systems, man and cybernetics-part A: systems and humans. 38(4): 818-831. https://doi.org/10.1109/TSMCA.2008.923086

Li, J.Q., Pan, Q.K., and Mao, K. 2014. Hybrid particle swarm optimization for hybrid flowshop scheduling problem with maintenance activities. The Scientific World Journal. 1-14. https://doi.org/10.1155/2014/596850

Liang, J.J., Qin, A.K., Suganthan, P.N., and Baskar, S. 2006. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Transactions on Evolutionary Computation. 10(3): 281-295. https://doi.org/10.1109/TEVC.2005.857610

Melnyk, S.A., Ghosh, S., and Ragatz, G.L. 1989. Tooling constraints and shop floor scheduling: a simulation study. Journal of Operations Management. 8(2): 69-89. https://doi.org/10.1016/0272-6963(89)90013-2

Moonsri, K., Sethanan, K., and Sangsawang, C. 2015. Metaheuristics for Scheduling Unrelated Parallel Machines with Sequence-Dependent Setup Time and Machine Eligibility. Chiang Mai University Journal of Natural Sciences Special Issue on Logistics and Supply Chain Systems. 14(4S): 431-446. https://doi.org/10.12982/cmujns.2015.0097

Nasir, M., Das, S., Maity, D., Sengupta, S., Halder, U., and Suganthan, P.N. 2012. A dynamic neighborhood learning based particle swarm optimizer for global numerical optimization. Information Sciences. 209: 16-36. https://doi.org/10.1016/j.ins.2012.04.028

Office of the Cane and Sugar Board. 2016. The annual report of sugarcane plantation and sugar production in 2015/2016. Retrieved from http://www.ocsb.go.th/upload/OCSBActivity/fileupload/8071-2689.pdf

Özpeynirci, S., Gökgür, B., and Hnich, B. 2016. Parallel machine scheduling with tool loading. Applied Mathematical Modeling. 40(9): 5660-5671. https://doi.org/10.1016/j.apm.2016.01.006

Pant, M., Thangaraj, R., Grosan, C., and Abraham, A. 2008, November. Hybrid differential evolution-particle swarm optimization algorithm for solving global optimization problems. In Digital Information Management, 2008. ICDIM 2008. Third International Conference on (pp. 18-24). IEEE. https://doi.org/10.1109/ICDIM.2008.4746766 

Prasara-A, J., and Gheewala, S.H. 2016. Sustainability of sugarcane cultivation: case study of selected sites in north-eastern Thailand. Journal of Cleaner Production. 134(1): 613-622.

Rahman, R.A., Santosa, B., and Wiratno, S.E. 2014. Hybrid Differential Evolution and Bottleneck Heuristic Algorithm to Solve Bi-Objective Hybrid Flow Shop Scheduling Unrelated Parallel Machines Problem. Proceeding of the 2014 International Conference on Industrial Engineering and Operations Management, January 7-9; Bali, Indonesia.

Sangsawang, C., Sethanan, K., Fujimoto, T., and Gen, M. 2015. Metaheuristics optimization approaches for two-stage reentrant flexible flow shop with blocking constraint. Expert Systems with Applications. 42(5): 2395-2410.

Sugar Research Australia. 2017. Precision Agriculture for the Sugarcane Industry. Retrieved from https://sugarresearch.com.au/wp-content/uploads/2017/02/Manual-Precision-Agriculture-for-the-Sugarcane-Industry.pdf

Santosa, B., and Riyanto, O.A.W. 2016. Hybrid Differential Evolution-Variable Neighborhood Search to Solve Multiobjective Hybrid Flowshop Scheduling with Job-Sequence Dependent Setup Time. In International Conference in Swarm Intelligence (pp. 587-598). Springer International Publishing.

Shi, Y., and Eberhart, R. 1998. May. A modified particle swarm optimizer. In Evolutionary Computation Proceedings, 1998. IEEE World Congress on Computational Intelligence., The 1998 IEEE International Conference on (pp. 69-73). IEEE.

Storn, R., and Price, K. 1997. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization. 11(4): pp.341-359. https://doi.org/10.1023/A:1008202821328

Tonge, V.G., and Kulkarni, P. 2013. July. Solving Permutation Flowshop Scheduling Problem Using Improved Differential Evolutionary Algorithm. In International Journal of Engineering Research and Technology. 2(10). ESRSA Publications.

Wang, W., & Hunsucker, J. L. (2003). An evaluation of the CDS heuristic in flow shops with multiple processors. Journal of the Chinese Institute of Industrial Engineers. 20(3): 295–304. https://doi.org/10.1080/10170660309509238

Widmer, M. 1991. Job shop scheduling with tooling constraints: a tabu search approach. Journal of the Operational Research Society 42(1): 75-82. https://doi.org/10.1057/jors.1991.9

Xu, D., Liu, M., Yin, Y., and Hao, J. 2013. Scheduling tool changes and special jobs on a single machine to minimize makespan. Omega. 41(2): 299-304. https://doi.org/10.1016/j.omega.2012.04.003

Yang, C., and Simon, D. 2005. August. A new particle swarm optimization technique. In Systems Engineering, 2005. ICSEng 2005. 18th International Conference on (pp. 164-169). IEEE. https://doi.org/10.1109/ICSENG.2005.9

Zeballos, L.J. 2010. A constraint programming approach to tool allocation and production scheduling in flexible manufacturing systems. Robotics and Computer Integrated Manufacturing. 26(6): 725-743. https://doi.org/10.1016/j.rcim.2010.04.005

Zeballos, L.J., Quiroga, O.D., and Henning, G.P. 2010. A constraint programming model for the scheduling of flexible manufacturing systems with machine and tool limitations. Engineering Applications of Artificial Intelligence. 23(2): 229-248. https://doi.org/10.1016/j.engappai.2009.07.002

Zhonghua, H., Haibo, S., and Chang, L. 2009. November. Differential evolution algorithm for the earliness tardiness hybrid flow shop scheduling problem. In Intelligent Information Technology Application, 2009. IITA 2009. Third International Symposium. (2: 188-193). IEEE. https://doi.org/10.1109/CSCWD. 2016.7565994

Zhou, Y.P. 2012. Optimization of flow shop scheduling problem using differential evolution and variable neighborhood search. In Advanced Materials Research. (590: 540-544). Trans Tech Publications. https://doi.org/10.4028/www.scientific.net/AMR.590.540