ABSTRACT
In early childhood education in rural areas, including ethnic minority areas, children’s folk games often play an important role in cultivating numerical thinking. The establishment of number sense is a concrete representation of the development of numerical thinking. Accordingly, this study evaluated the number sense of senior kindergarten and grade 1 students with and without the influence of playing folk games. The results showed that the groups of students exposed to the games were significantly superior to the non-influenced groups in counting, calculation, arithmetic cognition and number transformation, among other areas. Therefore, under the premise of the unbalanced development of education in rural China, it is necessary to emphasize the development and expansion of children’s folk games to reduce the delay in cultivating mathematical thinking.
Keywords: Rural education, Early childhood mathematics, Children’s folk games, Numerical thinking, Number sense.
INTRODUCTION
Due to geography, history and politics, economic development lags in parts of rural China, especially the areas of the southwest, northwest and northeast with minority or ethnic populations. With a weak educational foundation, inadequate investment in education and a lack of high-quality resources, the quality of teaching is in decline. The education gap to the more developed urban centers is growing, affecting rural development, including the ethnic areas. This gap includes mathematics education, and starts from early childhood.
The formation and development of numerical thinking is one of the goals of early mathematics education. However, the cultivation and develop- ment of numerical thinking is not limited to the classroom, and should be extended to daily life. Cultivating numerical thinking in rural daily life can complement classroom teaching, and make early childhood education more effective. Children’s folk games play an important role in linking these two: the classroom and daily life.
Johan Huizinga (1955), in pointing out the relationship between culture and play, meant the play element of culture, and not the play element in culture – “It was not my object to de- fine the place of play among all other manifestations of culture, but rather to ascertain how far culture itself bears the character of play.” (Foreword, p. 1) Mathematics education belongs to a part of culture, so its origin also bears the character of play. Research is limited on the relationship between children’s games and mathematics education. NAEYC & NCTM (2002) expressed, in their joint position statement, that people must “provide ample time, materials, and teacher support for children to engage in play, a context in which they explore and manipulate mathematical ideas with keen interest” (p. 10). Jennifer Taylor-Cox (2003) expressed, as with the concept of change, that children could construct knowledge about each of the major components of numerical thinking through play. They saw mathematical situations and structures as they compared the amounts of juice in each other’s cups. Furthermore, they also found algebra in stories, songs, poems and finger plays (pp. 14-21). Some Chinese scholars have proposed the educational value of traditional games and applications for young children (Qiu Xueqing,1997.
From the perspective of folk mathematics, many children’s folk games directly or indirectly involve numbers and graphics; these games can exert a subtle influence on the development of children’s number intuition, or number sense. Since Dantzig formally proposed the concept of number sense in 1954, it has become a widely used term in the fields of psychology and mathematics education. In China, it is first mentioned in Compulsory Education Mathematics Curriculum Standards (Trial version) in 2001. Here it mainly refers to general understand- ing of numbers and operations. These curriculum standards state that
...the number sense contains to understand the significance of the number; to use a variety of methods to represent the number; to grasp the relative size of number in a concreted context; to use the number to express and exchange information; to select the appropriate algorithm to solve the problem; to estimate the result of operation, and make a reasonable explanation for the results (Mathematics Curriculum Standard, 2001, p. 2).
For rural children, especially ethnic children, folk games can help them better develop this sense and meet the standards. The construction of number sense is a reflection of the acquisition of numerical thinking, which directly affects numerical prob- lem-solving ability. It is important for the development of high-level arithmetic and algebraic thinking.
For Bergeron and Herscovics (1990), ...the focus on what should be learnt in order to acquire numerical competence has moved further away from a view that emphasizes the mastery of particular concepts, procedures and their skilled application, towards a dispositional view of mathematical competence involving the integrated availability and flexible application of different components. This notion of disposition involves, besides availability of conceptual schemes and strategies, notions of inclination and sensitivity, as nicely reflected in the increasingly popular construct of “number sense”(or “numeracy”) (Ángel Gutiérrez et al., 2006, p. 72).
Numerical thinking involves the construction and expansion of numbers.
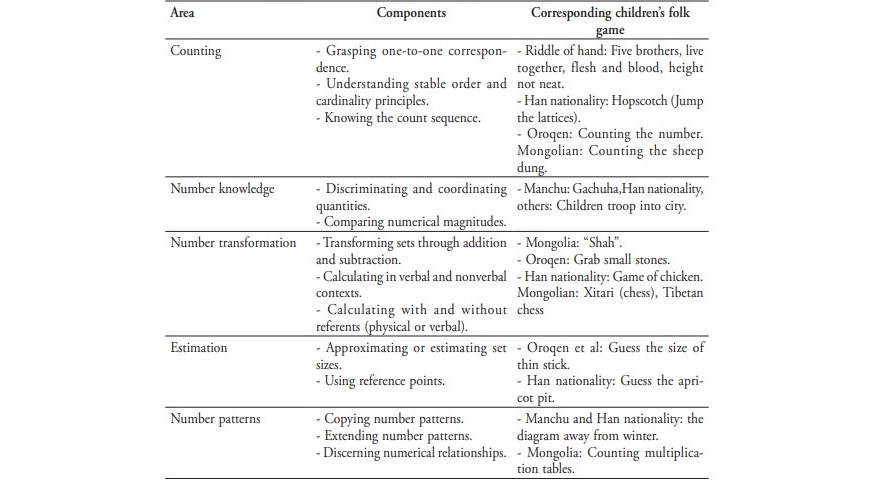
Jordan summarized the main components of number sense as follows: counting, number knowledge, number transformation, estimation and numerical patterns (Jordan et al., 2006, p. 154), most of which can be interpreted through children’s numerical folk games. The corresponding relationships between key elements of number sense and folk games in young children are shown in Table 1.
Content, type and game play of folk games are influenced by national social history, geography, customs, culture and morality, and reflect national social attributes, thus forming a certain cultural context. With the aid of the cultural tools, it can be seen that cultivating numerical thinking is closely linked with folklore. Chinese researchers have seldom emphasized the relationships between children’s games and the cultivation of numerical thinking. Incorporating folklore mathematical thinking in the math curriculum will not only allow students to experience the process of mathematics development in different cultural contexts, but also to follow the process of individual mathematical cognitive development (from concrete to abstract), so that students may have the opportunity to feel the essential attributes of mathematics as human culture. As a result, in the mathematics curriculum, folk math- ematics should be used as a supple- ment or the cornerstone of academic mathematics. This is an important prerequisite for the all-round develop- ment of children's early mathematical thinking.
table 1. Corresponding relationships between key elements of number sense and folk games in young children
Interpretation of concepts
In this research, rural area refers to the underdeveloped rural areas where the Han nationality lives, such as southwestern, northwestern and northeastern China. China is also a multi-ethnic country, with the majority of ethnic minorities living in these same rural areas. Children’s folk games refer to the ones children play together in early childhood, including the games of the Han nationality as well as minorities.
In mathematics education, number sense refers to a person’s general understanding of number and operations along with the ability and inclination to use this understanding in flexible ways to make mathematical judgments and operations (McIntosh et al., 1992, pp. 3). Number sense is difficult to define, but easy to recognize. Students with good number sense can transfer easily between the real world of quantities and the mathematical world of numbers and numerical expressions, invent their own procedures for conducting numerical operations, and represent the same number in multiple ways depending on the context and purpose of this representation.
Numerical thinking is based on the development of number sense, and the process of discovering useful connections between numerical analysis and other fields in computing. According to Verschaffel (2006), numerical thinking is related to several aspects of number concept and number sense: arithmetic operation, grasping the basic arithmetic facts, mental arithmetic, written calculation and application of numerical arithmetic knowledge and skills to solve word problems (p. 72). In fact, the development of arithmetic and algebraic thinking is a benefit of good numerical thinking.
In China, kindergartens are part of the preschool system of early chillhood education. Children ages 5 to 6 years old attend senior kindergarten; this grade level is often integrated into primary schools.
METHODOLOGY
Selected children’s folk games
The researchers selected some children’s folk games as case studies, including Gachuha, Hopscotch (tiao fangzi) and Guessing Riddle. Ga- chuha is derived from the shank or shinbone of sheep, pig, Mongolian gazelle, cattle or other animals, which is scraped clean of meat and fat through boiling. Mongolians call it "Shah"or "Shiah". Gachuha is sur- rounded by different shapes called "zhenr, beir lunr and kengr” in Pinyin of Chinese. The game of "Gachuha", a traditional source of entertainment for Mongolians, Manchu and Daur, is still popular in some areas of northern China. After selecting the case study games, we reviewed the literature (some of our case studies are sourced from the book “Chinese Folk Games and Sports”, Guo Panxi, Shanghai Sanlian Publishing House, 1996) and analyzed data to find the relationship between the cultivation of numerical thinking and children’s folk games under the context of social culture. Gachuha and hopscotch represent number sense games (Table 2).
Participants
Selected participants included: 1) 30 senior kindergarten children who could not count fluently nor understand number decomposition and combinations up to the number 10 and 2) 30 first grade students who failed in their examinations to understand the relationship between addition and simple multiplication. The students were from a nine-year coherent education school in Laoguan- tuo, Liao Zhong County, Shenyang Municipality, Liaoning Province in northeastern China. The school included Han, Manchu, Korean and other ethnicities. The participants were drawn from a senior kindergarten class of 60 students (25 boys, 35 girls) and a first grade class of 58 students (30 boys, 28 girls). The school, in the corresponding author’s hometown (which helped ensure the tests ran smoothly), was selected based upon the recommendation of the school mathematics resource teacher, who felt that the principal and teachers would be interested in participating.
table 2. The procedure of the children’s folk game and number representations in game play.

experimental procedure
The researchers conducted interviews and tests to collect data and analyze the relationship between children’s folk games and number sense. The participants were divided equally into an experimental and control group. The tests were conducted in April 2012, requiring four weeks to complete.
Interview
During the interview, the researcher asked the children questions about folk games (for example, “Do you know how to play the folk games Gachuha and hopscotch?”) and number sense.
tests aimed at senior kindergarten children
test K1: The researchers taught 15 children in an experimental group to play hopscotch, and let 15 children play common games in a control group during morning recess. After one school week (Monday-Friday), the researchers asked the children in both groups to count from 1 to 10.
test K2: The researchers then taught 15 children in an experimental group to play Gachuha, and let 15 children play common games in a control group during morning recess. After two school weeks, the researchers asked the children in both groups to decompose the number 5.
test K3: Finally, the researchers presented the students in the experimental group with the riddle: “The face of long hook, head hanging fan, four thick pillars, one little pigtail” (answer: elephant). The game was then further expanded by asking the students how many pillars and pigtails the two elephants had? The following day, the researchers presented the senior kindergarten children with two math problems (2+2=, 4+4=) to test whether the children understood addition through the riddle.
tests aimed at grade 1 primary school children
test P4: The researchers set the same procedure and conditions as test K3, but only explained the connection between addition and multiplication for the children in the control group while providing some mathematical examples. The next day, the researchers presented the grade 1 children with two math problems (2×2=, 4×2=) to test whether the children understood multiplication through the riddle game.
test P5: The game of “hopscotch” can be appropriately extended; the number on the lattice can change into the game’s score. The researchers divided the experimental group into two teams. When playing the game, team 1 raced team 2. After several rounds of the game, children calculated their scores (high score wins). The 15 students in the grade 1 experimental group played the game for one week. Afterward, the children in both the experimental and control groups were tested with 10 addition problems to check whether the game strengthened the children’s number transformation skills.
RESULTS
Interview results
According to the interviews, 95% and 80% of the students were not familiar with “Gachuha” and “hop- scotch”, respectively. They seldom knew others folk games.
test K1: Fourteen (of 15) children in the experimental group counted from 1 to 10 correctly. Only seven (of 15) in the control group did so.
test K2: With the teacher’s guidance, 13 (of 15) children in the experimental group decomposed the number 5 (2 and 3, 1 and 4, 3 and 2, 4 and 1) correctly. Only eight (of 15) children were able to do so in the control group.
test K3: In the experimental group, all of the children provided the correct answer; 13 children within 2 minutes and the other two children within 5 minutes. All of the children in the control group were also able to provide the correct answer, but after considerably more time than the experimental group.
test P4: Fourteen (of 15) students in the experimental group gave the correct answer to the problems (2×2=, 4×2=), but only nine (of 15) students did so in the control group (the remaining six students saw the multiplication problems as addition, so their answer was 6 in the second case). The students understood the meaning of multiplication and the relationship between addition and multiplication more easily in the experimental group than the control group.
test P5: Thirteen (of 15) students in the experimental group solved the addition problems correctly, while only nine (of 15) in the control group did so.
The test showed, whether senior kindergarten or grade 1 students, the experimental group that received instruction and practice in numerical folk games was superior to the control group in counting, calculation, arithmetic cognition and number transformation.
DISCUSSION
“Number sense primarily involves knowledge of and facility with numbers, knowledge of and facility with operations, applying knowledge of and facility with numbers and op- erations to computational settings” (Mcintosh, 1992, pp. 5-8). In cultivating number sense early in children, the first two are easy to develop and strengthen through folk games. This also provides an initial attempt for children to solve mathematical problems, seen as part of children’s cognitive development, enabling them to understand and solve more complex mathematical situations. Then, how do we strengthen number sense in rural areas through folk games, thus cultivating numerical thinking? An entertaining way is required through appropriate guidance; game components and frameworks are added and expanded upon in order to enhance the effect.
The former Soviet psychologist Vygotsky reasonably explained the dialectical relationship between folk games and children’s mathematical cognition. Lev Semyonovich Vygotsky (1987), although building on the interest in mental development in the field of cognitive psychology since Jean Piaget, thought that cognition could not be solely understood on the individual level, because psychological function and cognitive construction started from social relations and social interaction, gradually internalized by individuals; in other words, the development of mental capacity is the result of social interaction and social experience, first appearing at the level of social relations in human interaction, then entering the inner psychological level of children. Emotions driving imagination, illusion and achievement to non-realistic desires are often hidden in games; they can promote self-confidence, sense of control and social cognition and interaction.
In children’s folk games, the cultivation of numerical thinking is different from formal schooling; after all, the game’s main purpose is not for children to understand the specific significance of numbers, the size of numbers or the rules of computing from the perspective of numerical thinking. However, in the process of the psychological development of individuals at an early age and the development of numerical thinking, experience and common sense also play an irreplaceable role in the games, compared with formal school education. Representation of numerical thinking is mainly reflected in number cognition and expressions, as well as the reification of number sense components in the popular games. On the surface, it is superficial senses of the expressions that have the characteristics of intuition; but in the significance of enlightened education, the representations let children grasp and understand numbers, gradually building early numerical thinking. In this study, the children paid more attention to number recognition, counting and operators through game play. The pleasure of playing helped make abstract concepts more easily understood, which is particularly important for the establishment of early number sense. The folk games provided a natural and relaxed platform for cultivation and development of numerical thinking.
The identification and study of a single number is the primary form for accumulating number knowledge. When some children begin to recognize numbers, they do not correctly understand the number sequence. In the cultivation of numerical thinking, the sense of numerical sequence is particularly important, such as the number sequence of 10-0, or vice versa. The “count” not only refers to children’s earliest experiences with unidirectional counting, but also interval counting through the arrangement of even numbers (2, 4, 6, 8) or counting forward or backward from any number, which can be expanded in the game of “hopscotch” of the Manchu, Xibo minority in northeastern China. In test K1, the game strengthened children’s sense of number sequence, providing a sense of the variety of numerical presentations that would present themselves during formal schooling. With this game, the senior kindergarten children happily filled in the lattice with the appropriate numbers, jumped from number 1 to 9 with their friends, and more spontaneously counted the numbers than the control group. Through several rounds of play, the children easily remembered the number sequence and their number sense was repeatedly strengthened. Obviously, the game cultivated the children’s number intuition.
For number transformation, as in test K2, the game of “Gachuha” strengthened recognition and representation of numbers. The children in the experimental group learned to reinforce the changes of number in children’s logical thinking, and children also began to grasp the computing method of division. Even more so, the children grasped decomposition and re-composition. Decomposition or recomposition involves expressing a number in an equivalent form as a result of recognizing how this equivalent form facilitates operating on the recomposed numbers. For a younger student, decomposition or recomposition often manifests itself as the learner “invents” ways to solve arithmetic problems. When playing games, children always like to count the number of Gachuha. One 5-year old girl was unable to decompose the number 5 in class. However, when she played Gachuha, she successfully divided five Gachuha into (2 and 3) and (1 and 4). After she played several times, she was then able to decompose the number 5 when asked by the re- searcher. Obviously, she built a bridge between the quantity of Gachuha and the abstracted number. In fact, children manifest important intuitions about numbers and addition in both the invented procedure and in the ability to carry out the procedure of playing a game.
Imagination in game play enables languages and actions, or substitutes, deliver information to activate representation and diagraming in a child’s long-term memory, helping to re-structure them. However, games are the combined effect of information processing and control processes. Among them, perception and memory play essential roles. In test 3, the researcher presented the elephant riddle, which highlights cognition with the numbers 1, 2 and 4. As they children liked the lovely and gentle animal, they were able to think positively about the mathematics problem with the researcher’s guidance. A 5-year old boy said he liked solving mathematics problem like the elephant riddle, but did not like to solve the more traditional 4+4= or 2+2= in class. Other children in the experimental group agreed with this opinion. The children in the experimental group guessed the riddle. They understood the information to mobilize their imagination, perception and memory capacity. The numbers that appeared in the riddle were strengthened in the brain and children, in combination with life experience, guessed specific things related to the numbers.
Numbers appear in different contexts and may be expressed in a variety of symbolic and/or graphical representations. Number sense in- cludes the recognition that numbers take many forms and can be thought about and manipulated in many ways to benefit a particular purpose. For example, recognizing that 2+2+2+2 is the same as 4×2 is a useful conceptual connection between addition and multiplication. In test P4, through guessing the riddle, children were more inspired to grasp mathematical operations; they used their imagination to transform the riddle into solving the number problem. The students in grade 1 easily understood the relationship between addition and multiplication through guessing the riddle. In the experimental group, students used their imagination to count the elephant tails, ears and legs, which was more interesting to them than the dull mathematical equation. One eight-year-old girl in the experimental group did not understand the connection between addition and multiplication in class, often confusing the two. For example, when asked what is the answer of 3 multiplied by 2, she saw 3×2 as 3+2, so answered 5. In contrast, when she played the riddle of the elephant game, she grasped multiple relationships through counting two elephants’ tails, ears and legs, and was then able to solve the problems more quickly than the control group. Numbers can be represented in many different ways, with representations in some folk games providing a valuable tool for helping to develop mathematical understanding.
In terms of early childhood education, games help children develop and establish numerical thinking. For example, in test P5, the rules of “hopscotch” can be appropriately mediated. The number on the lattice can change into the game’s score. While playing hopscotch, the students of one team constantly add numbers to compare with the other team, in the happy and relaxed setting of the game. When children calculate their scores, the game strengthened their ability to use numbers and algorithms flexibly and provided continual practice. It was particularly important that they saw the game playing process as a happy and positive one. They were engaged when studying math problems through game play, and found the learning methodology more vivid and interesting than the traditional classroom instruction; they more easily understood the mathematical concepts.
For those folk games that contain or rely on underlying mathematical thinking or concepts, they can play a fundamental role in helping children cultivate an early number sense as well as promote numerical thinking.
CONCLUSION
Children everywhere, regardless of the natural environment or socioeco- nomic conditions, make use of time and local materials to create and play games. Many of these contain math- ematical components that can help develop numerical thinking, whether in isolation or in support of more formal classroom based methods. Us- ing folk games can help address some of the imbalances in early childhood education in rural China, while also stimulating traditional culture.
In addition, many children’s folk games have more educational value than many modern games. Not only do they play an important role in helping children develop numerical thinking, but they also teach children about local folk knowledge. However, under the premise of contemporary heritage and protection of intangi- ble cultural heritage, children’s folk games, especially those related to numbers, are slowly disappearing in China. These games can complement modern teaching methods, and arouse the attention of parents and teachers as children play and grow in the daily living space shared across generations as part of the national intangible culture.
ACKNOWLEDGEMENTS
The research was supported by a grant from the 2011 National Educa-tion Science Planning Fund in China

REFERENCES
In the research, some cases study of child’s folk games is sourced from the book “Chinese folk games and sports.” (Guo Panxi, Shanghai Sanlian Publishing House, 1996).
Gutiérrez, A., P. Boero. 2006. Handbook of research on the psychology of mathematics education: past, present and future Published by Sense Publishers, the Netherlands, pp.72.
Taylor-Cox, J. 2003). ALGEBRA in the Early Years? Young Children. January 2003. pp.14-21.
Huizinga, J. 1955. Homo Ludens: A Study of the Play Element in Culture, Beacon Press, Boston 1955 foreword, pp.1
Jordan, N.C,. D. Kaplan, O.L. Nabors, and M.N. Locuniak. 2006. Num- ber sense growth in kindergarten: A longitudinal investigation of children at risk for mathematics difficulties. Child Development, 77 (1):154. 10.1111/j.1467-8624.2006.00862.x
Verschaffel, L. 2006. Numerical Thinking Handbook of research on the psychology of mathematics education: past present and future. Eds: Ángel Gutiérrez, Paolo Boero Published by Sense Publishers, The Netherlands, 72.
McIntosh, A., J. Barbara, R. Reys, and E. Reys. 1992. A proposed Framework for Examining basic Number Sense [J]. For the Learning Mathematics, 12(3): 3, 5-8. FLM publishing Association, White Rock, British Columbia, Canada.
NAEYC & NCTM (National Council of Teachers of Mathematics). 2002. Early childhood mathematics: Promoting good beginnings. Joint position statement. pp. 10 Washington, DC: NAEYC and Reston, VA: NCTM. Online: www. naeyc.org/resources/position-statements/psmath.htm.
Xiang, P., and L. Zhongqi. 2010 (1). Core educational value and demand for the Traditional folk Games Preschool education research.
Qiu Xueqing. The educational value of Child’s Folk game. Journal of Educational Development (Preschool education edition), 1997(2).
Vygotsky, L.S. 1987. The collected works of L. S. Vygotsky: Vol. 1. Problems of general psychology (N. Minick, Trans.). New York: Plenum Press. 119-120.
The ministry of education, 2001. Full-time compulsory education mathematics curriculum standard (Trial version), Beijing normal university Press, 2.
