ABSTRACT

This study proposes that the strong correlation of the 3d electrons in Fe is an important key to understanding the stress dependence behavior of Curie temperature (T_c). We proved our proposed hypothesis using density functional theory (DFT) within an LSDA+U (local spin density approximation +U) framework. Applying LSDA+U correction increased both the magnetic moment and magnon energy. The increased magnon energy directly contributed to the higher magnitude of the calculated T_c (compared with LSDA). The acquired T_c (from LSDA and LSDA+U) decreased with increasing unit cell volume; this was consistent with previous studies. Although introducing an on-site Coulomb interaction yielded the same stress dependence trend of T_c compared with the LSDA results, increasing the T_c magnitude was more reasonable under meanfield approximation, suggesting that the strong interaction of the 3d electrons in Fe influenced this phenomenon.

Keywords: Stress dependence, Curie temperature, Body-centered cubic iron, Frozen spin spiral, Magnon, LSDA+U

INTRODUCTION

Curie temperature (T_c) is one of the most important and studied factors in magnetic-based applications. The most common material for studying magnetic properties is iron (Fe), because of its high T_c and low cost. The dependence of T_c on stress in Fe, particularly, at room temperature phase (bcc Fe), helps predict the magnetic order in storage devices at actual operational temperatures. Leger and Loriers-Susse (1972) reported the independence of T_c and stress; they showed that the magnetic phase transition remained at a given temperature, even when under stress. However, Morán et al. (2003) produced inconsistent results, concluding that the Heisenberg model might not correctly describe this phenomenon. Later, Körmann et al. (2009) reported good consistency between their calculated and experimental results. Thus, density functional theory (DFT) calculations appeared to clearly describe the independence of stress, although why their results improved upon Morán et al. (2003) has not been clarified.

Theoretically, Morán et al. (2003) and Körmann et al. (2009) used nearly identical methodologies, but obtained different results. Both calculated T_c by integrating magnon energy along a high symmetry path in the Brillouin zone (the so-called ‘frozen magnon’ approach) (Halilov et al., 1998). However, Körmann used an extremely high fixed cone angle (θ), while Morán used a low θ, the primary difference between the two and likely reason for the divergent results. An extremely high fixed cone angle, e.g., θ = 90°, implies a large spin state perturbation. This could change the magnitude of the atomic spin moment of each cone angle state (Jacobsson et al., 2013). The expansion of DFT total energy of each spin spiral state via Heisenberg model is valid under the assumption of constant atomic spin moment. Consequently, θ that is too high will breakdown the assumption. On the other hand, a small θ, while well supported by theory, will suffer from numerical inaccuracy and computational instability of the self-consistent field (SCF) calculation in practice. The best choice for θ with Fe is neither too high to breakdown the assumption, nor too low to cause numerical inaccuracy.

In addition to the choice of θ, a strong coulomb interaction should be included in the calculation when using materials composed of Fe (or other 3d transition metals), in particular, iron oxides. While the insertion of on-site coulomb interaction via U parameter may be excessive in the case of pure Fe, we hypothesize that this may be the key factor in the dependence of T_c on stress. Therefore, this study first determines the proper θ and then calculates T_c using LSDA (local spin density approximation). We also use LSDA+U to introduce strong electron correlation to investigate the dependence of T_c on stress.

MATERIALS AND METHODS

Theory and computational methods

The magnon calculation strategy in this study is based on the frozen magnon approach, in which the magnetic interactions are mapped to Heisenberg Hamiltonian of the form:

where J_ij is the exchange interaction and 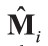 is the on-site atomic moment localized at atom i. The conventional Heisenberg model ignores the contribution from longitudinal motion of the spin moments. However, for the system under consideration, Ruban et al. (2007) has recently shown that the longitudinal fluctuation has only a minority effect on T_c that can be neglected.

This study takes into account the generalized Bloch’s theorem to perform self-consistent spin spiral calculations at different volumes, V. The spin spiral state of the system for a single magnetic atom per unit cell can be characterized via the moment:

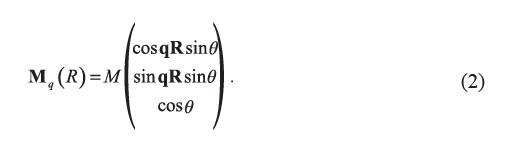
with q the position in reciprocal space, R the lattice vector, M the magnitude of the spin moment, and θ the cone angle of the spin wave. The perturbation of the spin state from the ordered magnetic ground state with a small θ (low-lying) could be considered as the magnetic quantized mode or magnon.

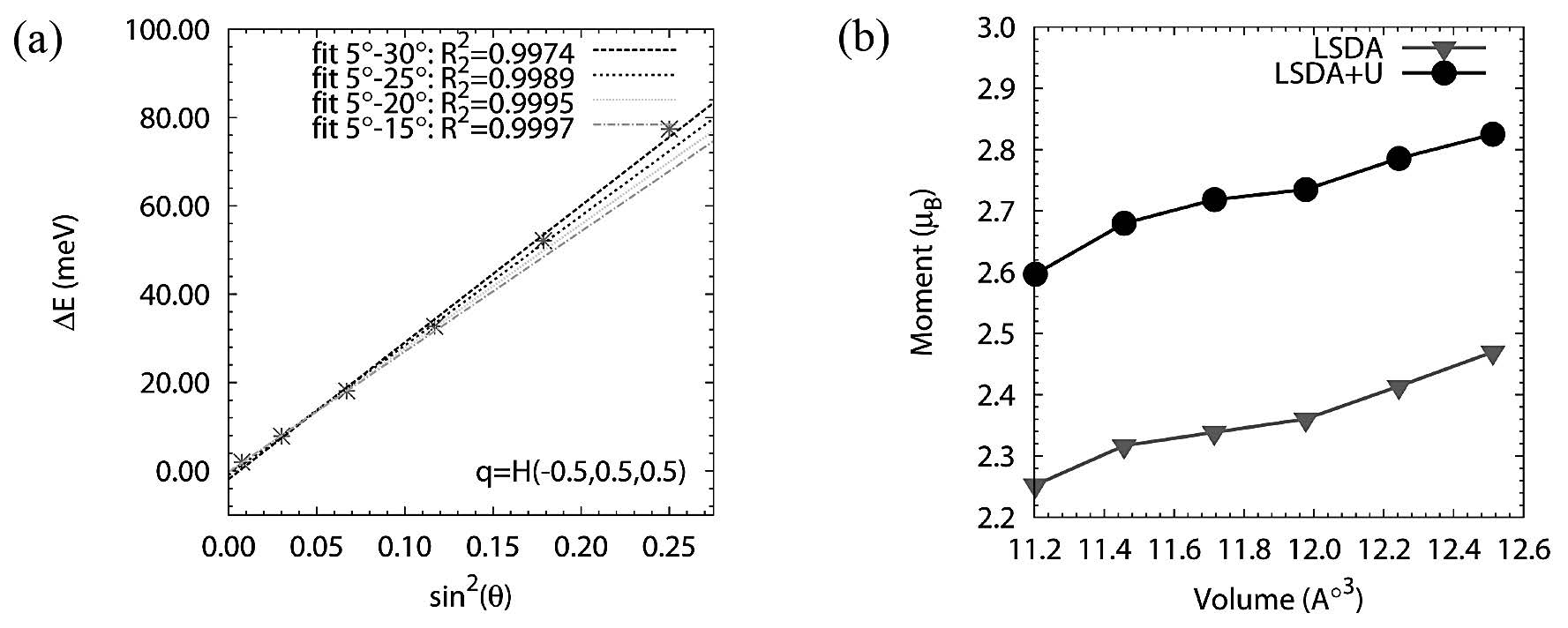
Figure 1. (a) The linear fitting between ΔE_q,θ and sin² (θ) (the red asterisk is the raw data, the dashed lines with different colors represent linear fitting in the labeled range of cone angle (θ)) and (b) the magnetic moment as a function of unit cell volume.

The total energy difference between the perturbed spin spirals and the ferromagnetic states of the system containing the single magnetic atom per unit cell, ΔE_q,θ can be attributed to the magnon energy (ωq(V)) of the system (Kübler, 2006; Jacobsson et al., 2013):

where M(V) is the volume dependent magnetic moment.

To choose θ, we first investigated the relation between ΔE_q,θ and sin²(θ), finding that the linear trend was acceptable with θ ranging up to 25° (R² ~ 0.999), as shown in Figure 1(a). Therefore, we selected θ = 25° as the fixed cone angle to use throughout this study.

We employed the mean-field approximation (MFA) derived from the Heisenberg model to obtain the Curie temperature (Pajda et al., 2001): 

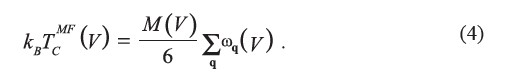
The dependence of T_c on stress σ, T_c(σ), is determined by the slope of T_c and V multiplied by the derivative of V with respect to σ, at T = T_c.

We obtained the total energies by the full-potential linearized augmented plane-wave method (FP-LAPW) as implemented within ELK package. We used 16×16×16 of k-point mesh in the irreducible Brillouin zone. The potential and density were expanded within a plane wave cut-off of |G| = 14/a₀ (a₀ is the Bohr radius), and R×|G+k| is restricted to 8a₀, where R is the muffin-tin radius of Fe (2.30 Bohr).

The calculations were performed using the LSDA and the LSDA+U. We used the parameters from Perdew-Wang (1992) for the LSDA function. For the LSDA+U calculation, the d-d interactions were counted into the localized part by adding the Hubbard term or the screened Coulomb and exchange parameters, i.e., U and J. The non-localized part was calculated in the same way as in LSDA. While many choices of U and J for bcc Fe exist, we chose the one calculated from the linear response calculation (Cococcioni and Gironcoli, 2005): U_eff ~ 2.2 eV. U_eff is the effective Hubbard parameter, including U and J. In all LSDA+U calculations, we took into account the double counting term by using the fully localized limit (FLL). To calculate magnon, we applied a small external magnetic field to constrain the spin spiral direction. Their energies were excluded from the total energy and this only controls the direction, i.e., the magnitude of the magnetic moment remained fully self-consistent.

RESULTS

Before performing the first principles calculation under the non-collinear spin spiral treatment of our system, we optimized the computational accuracy by considering Fe as a collinear magnetic system. The magnetic moment acquired from the collinear calculation (2.18 μ_B) agreed well with our experimental results of 2.20 μ_B (at 120 K) (Billas et al., 1993). We then performed the non-collinear calculations. At a fixed experimental volume, the non-collinear LSDA gave a magnetic moment of about 2.3 μ_B, while the non-collinear LSDA+U increased the magnetic moment (up to 15%); this was consistent with the theoretical work of Rollmann et al. (2004). The magnetic moments as a function of cell volume from both the LSDA and LSDA+_U calculations are shown in Figure 1(b).

The approximation in equation 3 allows us to characterize the magnon behavior of the given system. Our calculated magnon spectrum at fixed volume is shown in Figure 2(a). The results agreed quite well with Morán et al. (2003), in both magnitude and spectrum shape. From the LSDA results, Curie temperature calculated via magnon dispersion was consistent with our experimental results, although of a slightly lower magnitude. Our LSDA calculation predicted T_c of 1,030 K for bcc iron; the experimental results were 1,044 K. However, since LSDA+U treatment causes a higher magnon spectrum than bare LSDA (see Figure 2(a)), the theoretically predicted T_c obtained at +U was higher than that of bare LSDA. LSDA+U calculated T_c of about 1,400 K for this system.

To investigate the effect of stress on T_c, we calculated the magnon spectra at different volumes, ranging from 11.20 - 12.51 ų; this was a similar range to Morán et al. (2003) and Körmann et al. (2009). The magnon spectra at larger volumes were weaker than those at smaller volumes (as shown in Figure 2(a)). In contrast, we found that the magnetic moment increased with increasing volume (see Figure 1(b)).

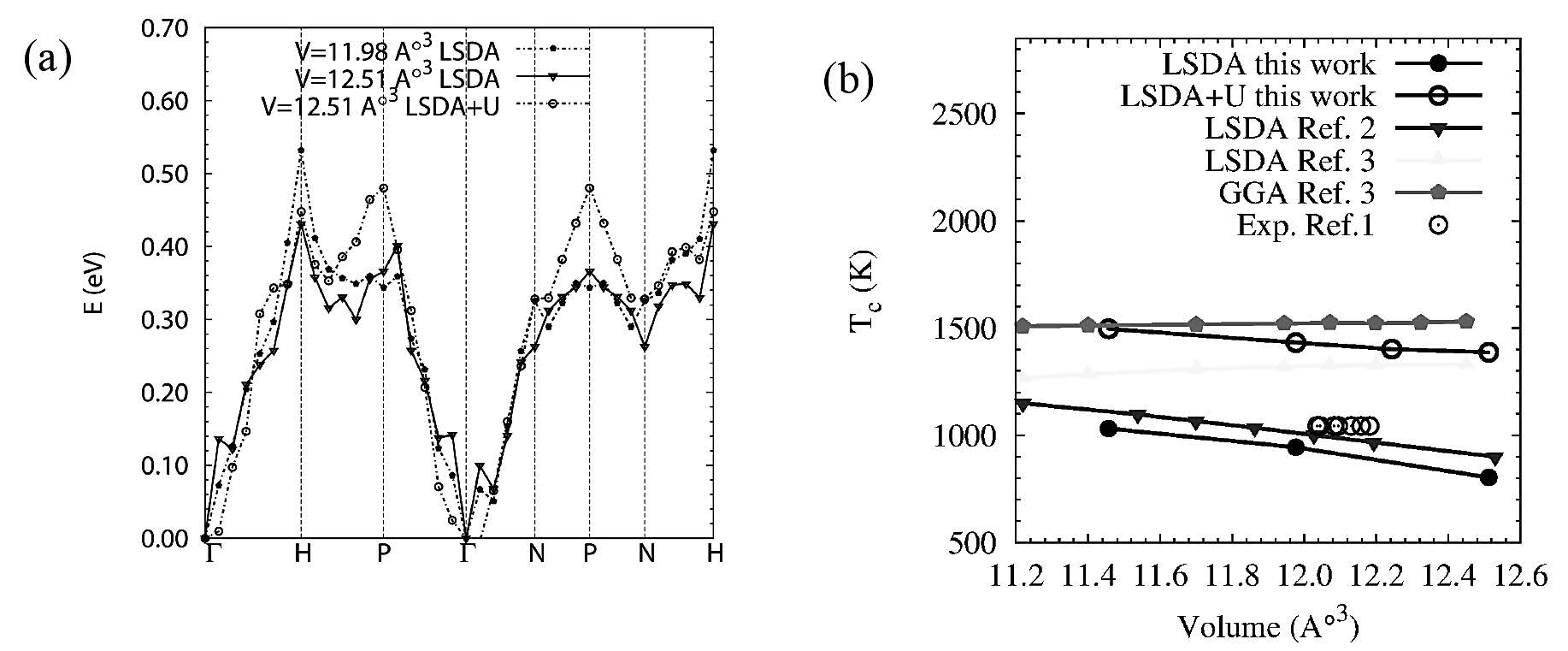
Figure 2. (a) Magnon spectrum from LSDA and LSDA+U at different unit cell volume and (b) the dependence of Curie temperature (T_c) on unit cell volume.

The relation between T_c and V calculated from LSDA and LSDA+U exhibited a linear trend with the decrease in T_c under an increasing unit cell volume. The Tc we calculated by LSDA+U and the GGA results of Körmann et al. (2009) were comparable. The combination of their GGA calculation and random phase approximation (RPA) accurately predicted their experimental results (Körmann et al., 2009).

DISCUSSION

The use of non-collinear spin spiral treatment (either with or without +U correction) moderately increased the magnitude of the calculated magnetic moment. This enhancement was induced by a small external magnetic field applied to constrain spin spiral cone angle. Although the use of a small enough external magnetic field led to a calculated magnetic moment with the same magnitude as the collinear one (and the experimental one), it may not be a sufficiently large fixed cone angle, and resulted in the instability of the SCF calculation. The Fe magnetic moments calculated using +U correction (either with collinear or non-collinear treatment) were higher than the experimental values (and higher than bare LSDA). This is because the Hubbard +U usually increases the spin splitting between majority and minority spin states (Tao et al., 2014). Thus, the magnetic moment, defined as the difference of electron density in majority and minority spin channels, is enhanced. This behavior of Hubbard +U correction has been shown to exist in 3d transition metals, as well as 4f transition metals, such as Gd (Tao et al., 2014).

Our LSDA results (at equilibrium volume) produced slightly lower T_c values than the experiment values. This was not reasonable, because we used mean-field approximation (MFA) (Pajda et al., 2001) that generally overestimates T_c compared to experimental measurements. The conventional MFA strongly overestimates T_c ; 1,414 K for bcc Fe (Liechtenstein et al., 1987; Pajda et al., 2001). Our results obtained using LSDA and MFA seemed to reproduce the experimental values, but also simultaneously displayed the inconsistency with the data reported in by Liechtenstein et al. (1987) and Pajda et al. (2001). This means that using only bare LSDA within a frozen magnon approach and MFA may not be sufficient to achieve reliable T_c results.

In contrast, combining LSDA+U with MFA produced T_c of about 1,400 K with a more acceptable consistency; these results agreed well with the GGA results of Körmann et al. (2009). Their GGA results analyzed with a more accurate scheme, i.e., random phase approximation (RPA), accurately predicted T_c (compared to experimental results). This implied that our LSDA+U could produce the same values as experimental results.

The magnitude of T_c as a function of cell volume (Figure 2(b)), with both LSDA and LSDA+U, was linear with a negative slope; this was consistent with Morán et al. (2003). Our calculation was based on DFT with LAPW method, which defines the wave function with spherical harmonics and a plane wave basis inside and outside the atomic sphere (defined by muffin-tin radius, R_mt); Morán et al. (2003) used the same method. Therefore, our T_c calculations should agree well with Morán et al. (2003), yet discrepencies occured. This may have been the result of different calculation parameters, e.g., the k-point mesh; they used 40×40×40, while we used 16×16×16. However, we found that using a 22×22×22 k-point mesh increased T_c about 20 K compared with that of a 16×16×16 k-point mesh (at V = 11.457 ų), while using R_mt of 2.40 bohr introduced a fluctuation on the order of 200-400 K. The fluctuation of T_c with respect to unit cell volume was suppressed by fixing R_mt to 2.30 bohr, the largest value without overlapping of the spherical harmonic wave functions in the equilibrium unit cell volume of Fe. Therefore, the calculation of T_c was more sensitive to the choice of R_mt than k-point mesh. With fixed R_mt throughout the calculations of different cell volumes; the interstitial electron charge was increased by the increasing of unit cell volume, while the electron charge inside R_mt was reduced. Because the constrained direction of the spin spiral state was applied only in R_mt, a lower electron charge inside the atomic sphere in the case of larger volume weakened the spin spiral effect, and resulted in lower T_c.

CONCLUSION

We aimed to determine whether adding strong electron correlation via on-site coulomb interaction (U parameter) would clarify the T_c dependence on stress. We found that the relationship between T_c and V calculated from LSDA and LSDA+U were linear, with a negative slope. The LSDA+U results produced higher T_c than those of pure LSDA. The calculated Tc from the +U correction was consistent with Körmann et al. (2009), which were able to reproduce the experimental results. Consequently, the Hubbard +U introduced into the system produced more realistic behaviors. The agreement of our results with previous research suggested that the strong interaction of the 3d electrons in Fe is a physical variable that plays an important role in T_c independence on stress.

ACKNOWLEDGEMENTS

The authors wish to acknowledge financial support from CMU Post-Doctoral Fellowship Program 2015, Chiang Mai University.

REFERENCES

Billas, I.M.L., Becker, J.A., Châtelain, A., and Heer, W.A. 1993. Magnetic moments of iron clusters with 25 to 700 atoms and their dependence on temperature. Physical Review Letters. 71: 4067-4070. doi: 10.1103/PhysRevLett.71.4067

Cococcioni, M., and Gironcoli, S. 2005. Linear response approach to the calculation of the effective interaction parameters in the LSDA+U method. Physical Review B. 71: 035105. doi: https://doi.org/10.1103/PhysRevB.71.035105

Halilov, S.V., Eschrig, H., Perlov, A.Y., and Oppeneer, P.M. 1998. Adiabatic spin dynamics from spin-density-functional theory: Application to Fe, Co, and Ni. Physical Review B. 58: 293-302. doi: https://doi.org/10.1103/Phys-RevB.58.293

Jacobsson, A., Sanyal, B., Ležaić, M., and Blügel, S. 2013. Exchange parameters and adiabatic magnon energies from spin-spiral calculations. Physical Review B. 88: 134427. doi: https://doi.org/10.1103/PhysRevB.88.134427

 
Körmann, F., Dick, A., Hickel, T., and Neugebauer, J. 2009. Pressure dependence of the Curie temperature in bcc iron studied by ab initio simulations. Physical Review B. 79: 184406.

Kübler, J., 2006. Ab initio estimates of the Curie temperature for magnetic compounds. Journal of Physics: Condensed Matter. 18: 9795. doi: 10.1088/0953-8984/18/43/003

Leger, J.M., Loriers-Susse, C., and Vodar, B. 1972. Pressure effect on the Curie temperatures of transition metals and alloys. 6: 4250-4261. doi: 10.1103/PhysRevB.6.4250

Liechtenstein, A.I., Katsnelson, M.I., Antropov, V.P., and Gubanov, V.A. 1987. Local spin density functional approach to the theory of exchange interactions in ferromagnetic metals and alloys. Journal of Magnetism and Magnetic Materials. 67: 65-74. https://doi.org/10.1016/0304-8853(87)90721-9

Morán, S., Ederer, C., and Fähnle, M. 2003. Ab initio electron theory for magnetism in Fe: Pressure dependence of spin-wave energies, exchange parameters, and Curie temperature. 67: 012407. doi: 10.1103/PhysRevB.67.012407

Pajda, M., Kudrnovský, J., Turek, I., Drchal, V., and Bruno, P. 2001. Ab initio calculations of exchange interactions, spin-wave stiffness constants, and Curie temperatures of Fe, Co, and Ni. Physical Review B. 64: 174402. doi: 10.1103/PhysRevB.64.174402

Perdew, J.P., and Wang, Y. 1992. Accurate and simple analytic representation of the electron-gas correlation energy. Physical Review B. 45: 13244-13249.

Rollmann, G., Rohrbach, A., Entel, P., and Hafner, J. 2004. First-principles calculation of the structure and magnetic phases of hematite. Physical Review B. 69: 165107. doi: 10.1103/PhysRevB.69.165107

Ruban, A.V., Khmelevskyi, S., Mohn, P., and Johansson, B. 2007. Temperature-induced longitudinal spin fluctuations in Fe and Ni. Physical Review B. 75: 054402. doi: https://doi.org/10.1103/PhysRevB.75.054402

Tao, K., Zhou, J., Sun, Q., Wang, Q., Stepanyuk, V.S., and Jena, P. 2014. Self-onsistent determination of Hubbard U for explaining the anomalous magnetism of the Gd1₃ cluster. Physical Review B. 89: 085103. doi: https://doi. org/10.1103/PhysRevB.89.085103